prof. dr. Andrej Bauer, FMF UL: Matematika je veda čistega uma
Prve dni januarja leta 2022 Ameriško združenje za matematiko (AMS) podeljuje nagrado, ki se imenuje po Leviju L. Conantu, profesorju računalniške matematike na Fakulteti za matematiko in fiziko (FMF) Univerze v Ljubljani (UL) prof. dr. Andreju Bauerju za članek »Five stages of accepting constructive mathematics«, Bulletin of the AMS, 54 (2017), 481-498.
Bauerjev članek je uvod v konstruktivno matematiko. S pojasnjevanjem osnovne predpostavke konstruktivne matematike, namreč da opustimo zakon o izključeni tretji možnosti – hitro potem razreši nekaj pogostih napak v njenem razumevanju. Pojasni Diaconescoujev rezultat, da iz aksioma izbire sledi izključena tretja možnost, nato pa dokaže, da je le-ta ekvivalentna izjavi, da so vse podmnožice končne množice (v konstruktivnem smislu) končne. Članek zlagoma predstavi nekaj osnovnih idej konstruktivizma. Bralca vodi skozi prve, otroške korake konstruktivne matematike, kjer že majhne variacije v formulaciji izrekov (sicer nezaznavne z nekonstruktivnega stališča) povzročijo velike spremembe.
Da osvajanje zapletenih znanj nima kraljevske poti, Bauer ponazori z izjavo: „S konstruktivno matematiko sem se prvič srečal med podiplomskim študijem, ko sem proučeval izračunljivost v analizi in topologiji. Še vedno se spomnim, kako težko se je bilo naučiti konstruktivnega razmišljanja in zatreti instinkte, ki jih je vgradilo klasično matematično urjenje.“
Mnogi matematiki so namreč skeptični ali celo sovražni do konstruktivizma. Bauerjev članek neposredno nagovarja take bralce in jih popelje na voden ogled skozi vrtove konstruktivne matematike. Čeprav je malo verjetno, da bo po prebiranju članka večina matematikov spremenila svoj osnovni način matematičnega delovanja, je zelo malo takih, ki jim članek ne bi predočil načina razmišljanja, ki ga do zdaj morda niso cenili – celo v povezavi z zadevami, za katere so mislili, da jih že razumejo.
Doseganje tako uglednih nagrad je plod leta dela in študija in kot je v Bauerjevem primeru, študija zahtevnih področij matematike. Po diplomi na Fakulteti za matematiko in fiziko (FMF) na UL, je doktoriral iz čiste in aplikativne logike na Carnegie Mellon University pod mentorstvom Dane S. Scotta. Zatem je preživel semester na Mittag-Leffler Institute v Stockholmu na Švedskem. Leta 2012 je bil član Institute for Advanced Study, kjer je sodeloval pri razvoju homotopske teorije tipov. Bauerjevo delo zajema temelje matematike, konstruktivno in izračunljivo matematiko, teorijo tipov, homotopsko teorijo tipov ter matematične principe programskih jezikov. Je soavtor knjige »Homotopy Type Theory: Univalent Foundations of Mathematics« in pobudnik knjižnice HoTT, ki je obsežna formalizacija homotopske teorije tipov v dokazovalnem pomočniku Coq. Znan je tudi po ključnih prispevkih na področju programiranja z algebraičnimi učinki in prestrezniki. V zadnjem času pa se ukvarja s teorijo tipov in načrtovanjem dokazovalnih pomočnikov.
(Spletna stran: https://www.ams.org/news?news_id=6827)
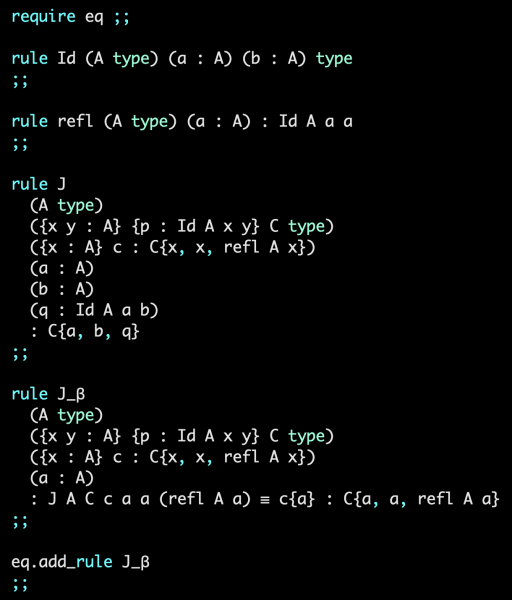
Raziskovalno delo s katerim se ukvarja dr. Bauer
Mnogi matematiki so namreč skeptični ali celo sovražni do konstruktivizma. Bauerjev članek neposredno nagovarja take bralce in jih popelje na voden ogled skozi vrtove konstruktivne matematike. Čeprav je malo verjetno, da bo po prebiranju članka večina matematikov spremenila svoj osnovni način matematičnega delovanja, je zelo malo takih, ki jim članek ne bi predočil načina razmišljanja, ki ga do zdaj morda niso cenili – celo v povezavi z zadevami, za katere so mislili, da jih že razumejo.
Doseganje tako uglednih nagrad je plod leta dela in študija in kot je v Bauerjevem primeru, študija zahtevnih področij matematike. Po diplomi na Fakulteti za matematiko in fiziko (FMF) na UL, je doktoriral iz čiste in aplikativne logike na Carnegie Mellon University pod mentorstvom Dane S. Scotta. Zatem je preživel semester na Mittag-Leffler Institute v Stockholmu na Švedskem. Leta 2012 je bil član Institute for Advanced Study, kjer je sodeloval pri razvoju homotopske teorije tipov. Bauerjevo delo zajema temelje matematike, konstruktivno in izračunljivo matematiko, teorijo tipov, homotopsko teorijo tipov ter matematične principe programskih jezikov. Je soavtor knjige »Homotopy Type Theory: Univalent Foundations of Mathematics« in pobudnik knjižnice HoTT, ki je obsežna formalizacija homotopske teorije tipov v dokazovalnem pomočniku Coq. Znan je tudi po ključnih prispevkih na področju programiranja z algebraičnimi učinki in prestrezniki. V zadnjem času pa se ukvarja s teorijo tipov in načrtovanjem dokazovalnih pomočnikov. (Spletna stran: https://www.ams.org/news?news_id=6827)
Ameriško matematično zduženje vam je podelilo izjemno nagrado, ki se imenuje po Leviju L. Conantu, za najboljši izpostavljeni članek objavljen v zadnjih petih letih naslovovom “Pet korakov k sprejemanju konstruktivne matematike”. Za širšo javnost pa taka nagrada in vsebina članka zahtevata nekaj več pojasnitev. Kdo je bil Levi L. Conant, po katerem se nagrada imenuje?
To je bil ameriški matematik, ki je živel na prelomu iz 19. v 20. stoletje, ukvarjal se je s trigonometrijo, je pa tudi napisal nekatere prve razprave, ker je proučeval številske sisteme domorodskih ljudstev Severne Amerike. S tem je delal tudi prve korake v antropologijo in etnologijo.
Naslov vašega članka Pet korakov k sprejemanju konstruktivne matematike na prvi pogled asociira z lahkotnostjo pri razumevanju prepletenih matematičnih vprašanj, ki se razkrivajo v ozadju. Lahko to pojasnite, ker nekoliko preseneča sam izraz konstruktivna matematika?
Tu se beseda konstruktivna bolj uporablja v inženirskem smislu konstrukcije. Namreč, kostruktivna matematika se od klasične matematike, ki jo učimo in prevladuje povsod, razlikuje po tem, da zahteva, da se vsak sklep in vsak matematični korak v nekem izvajanju matematičnih dokazov naredi na način, ki ga potem lahko tudi izvedemo z računanikom kot računalniški korak. Zato se imenuje konstrukcija v smislu, da je to nekakšen način, ki se da tudi dejansko izvesti. Od tod prihaja beseda konstruktivna. Res pa je, da so pravzaprav vsi načini matematike ustvarjalni. Po tem se ne razlikuje od klasične matematike, se pa mogoče razlikuje po tem, da ima konstruktivna matematika bolj neposredno povezavo z računalništvom in na tem mestu ustvarja neke nove povezave.
V utemeljitvi nagrade je zanimiv zapis …”čeprav je malo verjetno, da bo po prebiranju članka večina matematikov spremenila svoj osnovni način matematičnega delovanja, je zelo malo takih, ki jim članek ne bi predočil načina razmišljanja, ki ga do zdaj niso ocenili v povezavi z zadevami, za katere so mislili, da jih že razumejo”. Kako se matematiki ločite po načinu razmišljanja in delovanja?
Verjetno se najprej razlikujemo po tem, da se matematiki ukvarjajo z različnimi zvrstmi matematike. Eni z algebro, drugi z geometrijo, nekateri s kombinatoriko. Ko se leta in leta ukvarjaš z eno tako matematično vejo, razviješ neko intuicijo kako tam stvari delujejo, predstave imaš, ki niso potem neposredno uporabne na drugem področju matematike. Matematiki radi sami zase povedo, ali razmišljajo bolj z jezikom ali bolj vizualno. To je ena delitev, ki se pogosto omenja. Zase bi rekel, da kljub temu, da se ukvarjam z osnovami matematike, kjer pride zelo do izraza študij formalnih jezikov in sintakse, razmišljam bolj geometrijsko, o prostoru, ta način je bil meni vedno bolj privlačen. To je ena dimenzija, kjer se matematiki razlikujejo po svojem mišljenju in razmišljanju; to je bolj neformalna delitev. Na formalnem nivoju, o čemer tudi govori omenjeni komentar, pa gre za to, da pravzaprav vemo, da ni samo ena matematika možna, da ni samo eden možni sklop sklepanja aksiomov. Res pa je, da eden prevladuje in sicer ta, ki se je razvil v prvi polovici 20. stoletja. Možni so še drugi, ki imajo svojo uporabno vrednost. To morda vedo bolj specialisti, ki se ukvarjajo z osnovami matematike, medtem ko klasični matematiki, ki so dobili svojo klasično izobrazbo na klasični univerzi, poznajo predvsem to klasično matematiko. In to deluje vedno znotraj klasične matematike. Pri matematiku razvije nekatere prijeme, intuicije, njegove misli uhajajo v neke vzorce, kar pa se izkaže kot neprimerno, ko poskušamo delati matematiko še na kakšen drug način. In ravno to je težava pri razumevanju in sprejemanju teh drugih matematik, ki na prvi pogled izgledajo izjemno čudne, morda celo protislovne. In to je pravzaprav bistvo tega članka, kako nekomu predočiti nekaj, kar je po vseh letih njegovega izobraževanja na nek način tuje v razmišljanju.
A lahko matematik preklaplja iz sistema v sistem?
Moja izkušnja je, da lahko preklopi. Zato, da sam lahko preklapljam med različnimi načini, sistemi matematike, sem potreboval precej let treniga in izkušenj, da sem delal v enem, drugem, tretjem načinu. To je nekaj, kar zahteva matematika kot celoto, to je že tista specialnost, ki sem jo sam dosegel. In človeku ne ostane več ne prostora ne časa ne kapacitete v glavi, da bi zdaj poleg tega bil še strokovnjak za eno ozko vejo matematike. Je možno, a to ni nekaj, kar matematiki vse povprek počnejo. Zdi se mi, da gre v veliki meri tudi za to, kako so matematiki izobraženi. Matematika je vedno in povsod predstavljena kot nekaj, kar je zares objektivno, da ima objektiven pojem resnice. Resnica se v matematiki dokazuje, dokaz pa je neko zaporedje sklepov, ki ga lahko povsem mehansko preverjamo, torej imamo mehansko preverljiv pojem resnice. In s tem se matematika ponaša. Ampak ti sistemi matematike pa se razlikujejeo ravno v tem, kakšna so pravila za dokazovanje. In če potem spreminjate sistem dokazovanja, dobivate različne pojme dokazovanja in v tem lahko posledično različne matematične svetove s svojimi resnicami. In to niso svetovi, ki so popolnoma različni med sabo, so si zelo podobni. Razlike morda opazi šele študent višjega letnika. Skratka, možno je tako razmišljati, ampak navadni matematik zaradi svoje izobrazbe, zaradi tega, s čemer se ukvarja, enostavno nima te izkušnje, da bi to lahko kar tako počel.
Kaj pa tako priznanje pomeni za matematika, tako v kontekstu njegovega dela in zaveze k nadaljnemu raziskovanju, a hkrati pomena za ožjo in širšo matematično skupnost?
Vsekakor je to neko zelo dobrodošlo osebno priznanje zame. Dobil sem precej pozitivnih odzivov od te skupnosti matematikov, ki se ukvarjajo s konstruktivno matematiko, ker to je relativno majhna skupnost znotraj matematike in so veseli, da so izpostavljeni, da so vidni. Zagotovo je tu še element tega, da je to del tudi slovenske matematike vidne na mednarodnem področju. Moram pa povedati, da je slovenska matematika prisotna na mednarodnem področju že tako in tako v tem številu v katerem lahko je. Tudi moji kolegi so pred časom dobili primerljive nagrade istega društva, čeprav to sicer ni neka stalnica, smo pa zelo veseli tega. Vse to nas potem postavlja nekako bolj vidno v matematični svet, znotraj Slovenije pa je nagrada opozorila širšo javnost, da smo tukaj.
To sprašujem tudi ob asociaciji primera ruskega matematika Grigorija Perelmana, ki je ob rešitvi Poincaréjeve domneve leta 2004 zavrnil Fieldsovo medaljo in prekinil takorekoč s poklicem matematika. Sam potem ni dajal izjav, o njegovi odločitvi pa je spregovoril Mihael Gromov s pojasnilom…”Če želite delati odlično, morate imeti čisti um, da lahko razmišljate o matematiki. Idealni znanstvenik se ukvarja z znanostjo in se ne vpleta v nič drugega. In Perelman, ki je imel visoka moralna načela, je deloval nekonformistično , kar v skupnosti ni vedno priljubljeno, čeprav bi to moralo biti pravilo. In za matematiko velja, da je veda čistega uma.” Lahko tak način delovanja in razmišljanja vpliva tudi na osebnostne poteze?
Mislim, da sta tu dva nivoja. Prvič, če imamo matematika, genija, ki potrebuje mir, ki deluje na tak način kot je Perelman, ki je rešil enega najtežjih, najbolj znanih odprtih matematičnih problemov, kar gotovo ni bilo lahko, taki matematiki gotovo so in je dobro, da najdejo svoje mesto v matematični družbi, kjer zares lahko delajo. Težava pa je, kako prepoznati take, da jim to lahko omogočiš. Na drugem nivoju pa vsekakor ni res, da bo matematika kot človeška aktivnost lahko delovala na ta način, da bodo vsi matematiki nekonformistični in ne bodo hoteli imeti nobenega opravka z realnim svetom. To se enostavno ne bo zgodilo. Matematika je človeška aktivnost tako kot druge aktivnosti družbe. Potrebujemo piramido in na enega Perelmana imamo petsto matematikov, ki so vpleteni v družbo, ki razmišljajo o tem, od kje bo prišel denar, v kakšni stavbi bomo živeli, a bo ogrevanje,.. skratka, o vseh tistih trivialnih stvareh v življenju, za katere je potrebno poskrbeti. Moj pogled je tak, da tisto, kar bogati matematično družbo, je bolj raznolikost stvari in zavedati se je treba, da ob Perelmanu ali za njim stoji veliko drugih ljudi, recimo takih, ki radi poučujejo. Kje pa se je Perelman naučil vso to matematiko, bi se kaj naučil, če bi vsi njegovi učitelji bili taki kot je bil on? Bi imel kakšno priložnost, da bi se karkoli naučil, verjetno ne. In se je treba zavedati, da je tak genij, ki stoji kot zvezda na nebu, v resnici podprt s celo infrastrukturo in nekdo mora tudi za to poskrbeti.
V laičnem govoru slišimo kar nekaj trditev, kaj vse naj bi ponujalo matematično razmišljanje, da je dobro za možgane: da pomaga pri urejanju osebnih financ, da izboljša reševanje vsakdanjih problemov, da omogoča tudi boljše razumevanje sveta ter pomaga pri razumevanju drugih akademskih disciplin. Se vam zdi to pretiravnje?
Nekatere od teh postavk so morda samo zdrav razum in matematika res pomaga k temu, da ima človek res bolj zdrav razum v smislu, da se ne boji razmišljati, da ve, da z razmišljanjem lahko daleč prideš. Tiste stvari z urejanjem financ pa je bolj taka tehnična veščina, ki se je naučiš do petega razreda, če si dober v matematiki, če ne, pa se je moraš malo kasneje.
Že v stari Grčiji je matematika omogočila oblikovati mentalno disciplino, ki je potrebna tudi za druge discipline. Tako je recimo Feynman rekel, da tisti, ki ne znajo matematike, težko dobijo pravi občutek za lepoto najgloblje narave. To je zanimiva povezava. Tudi Feynman je bil zvezda.
Feynman je bil fizik in matematika je jezik fizike, je medij, v katerem se fiziki izražajo. In če fiziku vzameš matematiko je verjatno tako, kot če slikarju vzameš barve. Za fizika in ostale naravoslovne znanosti matematika predstavlja samo orodje, podlago, ki omogoča razmišljanje, prave vrste abstrakcije, ki potem živijo v Feynmanovih mislih, v mislih znanstvenika.
Čeprav je matematična veda danes najbolj v ospredju, pa nahajamo tudi pri poznavalcih včasih skepso, zlasti v tistih primerih, ko matematični modeli lahko odstopajo od realnih spremeb. Je kritična distanca do teh modelov na mestu?
Če govorimo o raznih napovednih modelih, statističnih modelih, kjer modeliramo neke dogodke v družbi ali napovedujemo kakšne stvari, se je potrebno zavedati, kaj statistika ponuja in česa ne. Tu se srečamo s splošnim razumevanjem javnosti o tem, kaj znanost sploh ponuja in česa ne. Mislim, da je zelo pomembno povedati, da znanost ni vsemogočna, je pa presneto dobro orodje še posebno v primerjavi z vsem ostalim, kar smo v zgodovini poskušali in naredili. In stvari niso enostavne, nihče ne more pričakovati, da bo nek znanstvenik na televiziji napovedal prihodnost, ker je ne bo, recimo epidemije. Napovedne modele oziroma gibanja, je potrebno pravilno razumeti. Vprašanje pa je, kdaj imajo ljudje priložnost razumeti, kaj je sploh pomen matematičnih modelov. Osnovno spoznanje, ki mora veljati je to, da se ljudje zavedajo, da so ti modeli veliko, veliko boljši kot govorice na cesti, kot pričakovanja ali vedeževanja. So neprimerno boljši in uporabni. Niso pa idealni, to ni napovedovanje prihodnosti. Treba jih je znati pravilno razumeti. In če poslušate znanstvenike, ki te modele razlagajo v javnosti, nihče ne bo rekel, da je to napoved prihodnosti. Te izjave ne boste slišali.
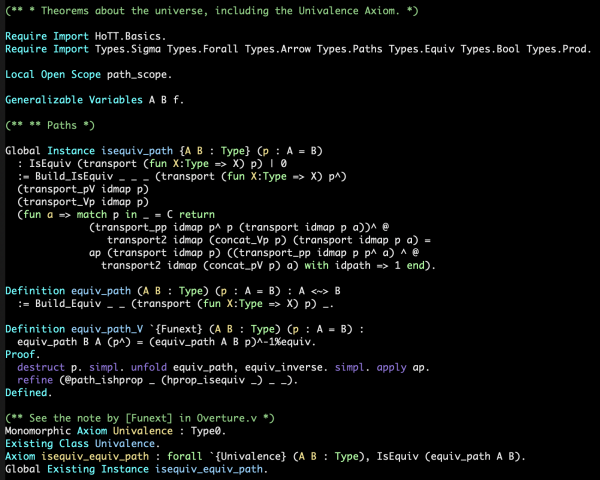
Slika prikazuje delček homotopske teorije tipov
Glede na to, da se veliko časa gibljeva okrog sintagme, da je matematika veda čistega uma, si marsikdo želi, da bi bili matematiki danes bolj vidni, bolj prezentni v prostoru. Ob tem pa ne gre spregledati podatkov v Eurobarometru, ki se kažejo problematični ali kar sramotni za Slovenijo. Če se osredotočiva predvsem na znanost smo pri vrhu z mnenji (48%), da so znanstveniki preveč ozkogledi, nemoralni, pri zaupanju v znanost pa se je Slovenija umestila kar na zadnje mesto. Skoraj polovica vprašanih zavrača njeno avtoriteto, četrtina pa niti ne ve, kaj naj si o tem misli. Zakaj je prišlo do take degradacije in prezira intelektualnih dejavnosti? Vi kot profesor ne morete biti brezbrižni do teh vprašanj, saj kot intelektualec z mednarodno reputacijo tudi oblikujete in socializirate prihodnji rod znanstvenikov?
Vsekakor ne morem biti brezbrižen, vprašanje pa je, kako se lahko borim proti temu, da sem resigniran. Nujno je, da znanstveniki sprevidijo, da je kljub vsemu treba delati na tem, da se komunicira z javnostjo, da se z njo oblikuje nek zdrav odnos. Tega ne moremo graditi sami, to lahko gradimo samo s pomočjo medijev, kvalitetnih medijev, ki vedo, kako se to dela. Zakaj so taka odklonilna mnenja, pa bi rekel, da je razlogov veliko. Spraševal bi se, kaj je potrebno spremeniti v šolskih procesih in v izobraževanju ljudi, dobiti vpogled v način, kako znanost deluje, da bodo ljudje razumeli kaj znanost je in kaj ni. Ker pa vsi ne moremo biti znanstveniki je zato pamento, da smo odprti, da komuniciramo in skušamo vztrajno skozi leta izboljšati šolski sistem. Zakaj pa so take razmere kot so, je potrebno vprašati tudi družboslovce, humaniste.
Vendar, poglejte okrog sebe, znanost je spremenila vaše življenje. Ne morete niti pet minut živeti v modernem svetu, ne da bi pri tem našteli deset znanstvenih dosežkov, ki so očitni že pri sedenju na stolu. A potem resno mislite, da vam želijo znanstveniki škoditi in ali resno mislite, da lahko komu drugemu zaupate bolj kot pa ljudem, ki so vam omogočili lagodnost življenja, napredek v medicini itd.? Če tem ljudem ne boste zaupali, komu pa potem boste.
Matematika še danes velja, morda bolj kot druge vede, za samotarsko znanost. Sodobna znanost pa je korporativna in zahteva tudi tekmovanje med znanstvenimi ekipami. Samohodcev takorekoč ni več. Kako vi to doživljate?
Ni znanost tista, ki zahteva korporativnost, to so financerji. Znanstveniki, prepuščeni sami sebi, se združujejo v kolaboracije, ne pa v tekmovanje drugega z drugim. To so predvsem zunanji elementi. Kar pa zadeva mnenja, da velja matematika nekako za samotarsko aktivnost, je bilo zgodovinsko precej res. Danes pa kažejo tudi statistike, da se število soavtorjev na članek v povprečju na matematiki dviguje. To govorim za čisto matematiko, da ne omenjamo apliktivne matematike, ki posega v računalništvo ali inženirstvo. Tu pa takoj vidite, da ni bistvene razlike z ostalimi vedami in matematični projekti zahtevajo tudi ekipe ljudi. Tu je še eden zelo zanimiv element…romantičen pogled, da je matematik sam v laboratoriju nekaj razmišlja in s svojim umom nekaj dojema. Ampak prav na področju, s kateim se sam ukvarjam, govorimo o barieri enega uma. Namreč, ukvarjam se s tem, kako z računalniki obogatiti raziskovalno matematiko in jo podpreti na tak način, kot so računalniki pomagali napredku pri šahu. Računalniki so danes boljši od vseh šahistov na svetu in pri matematiki bi bilo izjemno dobro, če bi lahko bolj pomagali pri razvoju matematike. In slej ko prej bo matematika naletela na bariero enega uma, se pravi, da ljudje ne bodo mogli delati matematike. Matematika je omejena s tem, kar lahko en matematik dojame in na nivo abstrakcije in količine tehničnih detajlov, ki jih lahko bolj ali manj en človek razume. Skupina matematikov ne more narediti nekih matematičnih rezultatov, če ni nikjer nikogar, ki bi zadevo razumel kot celoto. Mnogi bi rekli, da je to pravzaprav poanta matematike, matematiko delajo zato, da jo razumejo. Če pa pogledate kako delujejo druge vede, kjer je bolj naravno imeti ogromne projekte, pa zgraditi v Cernu velik pospeševalnik in razmišljate, kako bi matematiki lahko delovali na tem nivoju, vidite, da se morajo zgoditi neki premiki. In tak pogled na matematika, ki sam v pisarni nekaj piše in je velik genij in bo rešil človeštvo, se bo sicer še dogajal. Dogajalo pa se bo še veliko drugega, drugačnega razvoja, kjer bomo šli izrazito bolj v skupinsko delo s pomočjo računalnikov, ki nam bodo pomagali preseči bariero enega uma.
Z razvojem interneta so se stvari popolnoma spremenile in svet je postal nekako pošastna vas z naraščajočo populacijo nezadovoljnežev, visljivih bedakov, abderitov. In v takem svetu izjemni možgani štrlijo preveč ven in jih je potrebno utišati. Kako se vi spopadate s tem?
No, na Twitterju je gumbek, kjer svoj balonček očistite. To ima dobre in slabe lastnosti. Vsekakor se mi zdi, da je potrebno na socialnih medijih vzdrževati nek normalen nivo komunikacije in osnovne civiliziranosti. Če bi se take pritlehnosti v komunikaciji dogajale v živo na forumih, omizjih, razpravah, bi take ljudi varnostnik pospremil s prizorišča. Nihče jih ne bi prenašal. To so vzorci obnašanja in pravila družbenega vedenja, ki so v človeški družbi z razlogom. Danes pa so socialna omrežja bolj ali manj divji zahod, kjer je vse možno, vendar se bomo sčasoma le naučili in socializirali.
Na tehnološki razvoj pa vsi stavimo kot odrešujoč. In zdaj se kaže, da so to kvantne znanosti, umetna inteligenca. V kakšnem smislu pa bi se umetna inteligenca lahko približala razumevanju našega uma?
Tu se je potrebno vprašati, kaj je v naslednjem desetletju najbolj obetavno in kje so bili zadnji preboji. V devetdesetih letih in nekoliko kasneje se je veliko govorilo o genetskem inženirstvu, o genski znanosti, biomedicini…, kar je še zmeraj zelo prisotno. Trenutno nas ta znanost rešuje velike epidemije in to so dosežki, ki niso bili narejeni v enem letu ampak v zadnjih desetletjih. Kar zadeva kvantne računalnike, pa zelo dobro razumemo, kaj lahko od njih pričakujemo. Vemo, da se bodo nekateri računski postopki neznansko pohitrili z njihovo pomočjo, pridobili bomo možnost dešifriranja kakšnih starih sporočil, ki so nekje shranjena, nekatere računske probleme pa bomo zelo učinkovito reševali. Niso pa kvantni računalniki odgovor na vse. Nekaterih računskih postopkov ne znamo implementirati na hitro z računalniki, kakšnih se v bistvu tudi ne da. Vemo, da bodo prinesli velik preboj, bo pa klasično računalništvo še vedno ostalo pomebno. Kvantne računalnike je potrebno razumeti kot neke vrste impresivne zmožnosti računanja, vendar to ni tak preboj, da bi rekel, da bo to neka nova paradigma računanja.
Ko se je umetna inteligenca pojavila, so strokovnjaki začeli raziskovati lastno pamet, lastno kognicijo, kar smo prej doživljali kot danost samo po sebi. Tako raziskovanje je seveda zelo atraktivno. Bo z algoritmi možno implementirati spoznanja kognicije?
Seveda se ponujajo primerjave s tem, kako deluje človeški um, kakšne so kognitivne sposobnosti ljudi in na drugi strani raznih inteligentnih sistemov, predvsem zato, ker vidimo, da rešujejo podobne probleme…človek vozi avto, računalnik vozi avto, človek igra šah, računalnik igra šah, človek na fotografiji prepozna ali je mačka ali pes, tudi računalnik to zna. Ideje, da bo umetna inteligenca dosegla tako razvojno stopnjo, ki bo taka kot človek, po človeški podobi, so bile seveda prisotne že v začetku razvoja umetne inteligence , nekje v sedemdesetih letih. In kolikor je meni znano, se je nekje v osemdesetih, devetdesetih letih prepoznalo dejstvo, da pravzaprav ta idealni cilj umetne inteligence za enkrat še ni dosegljiv in mogoče še niti ni jasno, kakšen je. In raziskave so se bolj usmerile v reševanje parcialnih problemov umetne inteligence, kjer se je gradilo sisteme, ki so znali delati eno stvar dobro, recimo prepoznavati vsebino slike, prepoznavati govor, voditi pogovor s človekom v omejenem kontekstu. To je ta analitični pristop znanosti, kjer ni potrebno nekega problema rešiti v celoti, gre za parcialne probleme in to je pripeljalo do velikih uspehov. Še eno pomembno spoznanje pa je bilo to, da se v resnici lahko ogromno doseže, če se ne insistira, da so neki sistemi povsem samostojni, da so kot človek, ampak da sodelujejo s človekom. Npr. v medicini lahko dosežete dosti več, če ponudite pravo vrsto orodij, podprtih z umetno inteligenco strokovnjaku, da sodelujeta, kot pa če skušate skopirati strokovnjaka. Tudi če ga boste skopirali, ga nihče ne bo hotel uporabljati v medicini. Kdo se bo pa hotel pogovarjati z računalnikom, ko bo prišel k zdravniku? Ta vprašanja umetne inteligence se že precej dobro razumejo, idealnih predstav ni več. Se pa vedno znova sprašujemo, kdaj pa bomo dosegli nivo, ko se bodo vsi ti podsistemi umetne ineteligence sestavili skupaj in bomo ljudje te sisteme dojemali kot nekaj, kar nam lahko parira. Še vedno nismo blizu. Pet ali šest letni otrok, ko mu preberete pravljico, bo imel sposobnost razumevanja pravljice, ki je za magnitudo večja kar pričakujemo lahko od sistemov, ki so nam danes na voljo. Kaj šele, če postavljate umetne inteligentne sisteme v neke neznane situacije. In tu se moramo še veliko naučiti. Je pa res, da se ta vprašanja, kaj je človeški um, kaj je kognicija, selijo vedno bolj od filozofskih vprašanj k vprašanjem tehnike. In tehnika prenaša svoje poglede na celotno zadevo, ki so včasih zelo drugačni od teh klasičnih
Že prej ste rekli, da matematiki niste napovedovalci prihodnosti, pa se mi vendarle zdi, da obvladujete kategorialni aparat izpostavljene znanstvene vede in so vaše ocene glede prihodnjega razvoja toliko bolj lahko dragocene. Ste kdaj razmišljali o tem?
Težko boste našli matematika, ki vam bo napovedoval prihodnost ali pa vam dajal ocene glede prihodnosti. Mogoče lahko povem, da smo matematiki, pavšalno rečeno, nagnjeni k nekaterim zadevam, ki mogoče pa le pridejo prav. Prva je ta, da smo natrenirani, da vedno razmišljamo o patoloških možnostih. Obremenjeni smo s tem, da če trdimo, da je nekaj res, mora biti res v absolutnem smislu ne glede na kakšne patološke skrajne primere in to privede v zavedanje, da hitro pridemo v situacijo, ki je v osnovi neznana. In to je še ena stvar, s katero se matematik srečuje. Vi rešujete matematične probleme in ne veste, kaj bi naredili, vam ni znano in to rešujete lahko mesec ali leta in potem se naučite živeti tudi s spoznajem, da je neznaje oziroma nepoznavanje stvari pravzaprav norma. To je tisto, kar je normalno. In če vas v luči tega nekdo vpraša kakšne so napovedi za prihodnost, ne boste napovedali absolutnih napovedi, povedali pa boste nekakšne kvalificirane omejene presoje o tem, kaj bi se znalo zgoditi. Seveda je to težko napovedovati, ker gre za kompleksne sisteme. In matematik lahko iz svojih izkušenj z dinamičnimi sistemi res uvidi kaj zares pomeni kompleksnost in da je nenapovedljivo v tehničnem, v matematičnem smislu obnašanje nekega sistema nenapovedljivo. In ti sistemi niso izjema, so pravilo na mnogih področjih, v fiziki, v znanosti in ni nobenega dvoma, da je tudi v družbi tako. V luči tega potem res lahko svarimo o previdnosti v kaj lahko verjamete in kdaj morate kakšne razlage relativizirati.
Foto: dr. Andrej Bauer/osebni arhiv






